Το πρόβλημα της Βασιλείας και η κβάντωση της ακτινοβολίας
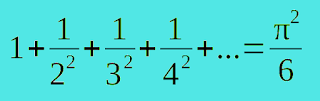
"Να εκφραστεί το άθροισμα των τετραγώνων των αντίστροφων φυσικών αριθμών σε κλειστή μορφή".
Αυτή ήταν περίπου η διατύπωση του προβλήματος της Βασιλείας, το οποίο διατυπώθηκε από τον Pietro Mengoli το 1650. Η λύση δόθηκε από τον Euler το 1734 και γι αυτό ονομάστηκε έτσι (η Βασιλεία ήταν η γενέτειρα του Euler).
Σε απλά Ελληνικά η διατύπωση του προβλήματος είναι: Γράψτε σε κλειστή μορφή το άθροισμα

δηλαδή βρείτε την ακριβή έκφραση αυτού του άπειρου αθροίσματος. Το αποτέλεσμα 1,644934... είναι ανοιχτή μορφή αφού μπορούμε να συνεχίσουμε να βρίσκουμε ψηφία επ'άπειρον.
Έχει ενδιαφέρον να ακολουθήσουμε τη σκέψη του Euler. Πρώτα απέδειξε ότι το άθροισμα συγκλίνει δηλαδή ότι όσο περισσότερους όρους προσθέτουμε τόσο περισσότερο πλησιάζουμε σε κάποιο πραγματικό αριθμό οπότε το άθροισμα δεν μεγαλώνει ώστε να γίνει άπειρο. Στο σημείο αυτό να επισημάνω ότι το άθροισμα

αποκλίνει, δηλαδή όσο προσθέτουμε όρους το άθροισμα μεγαλώνει απεριόριστα. Η τελευταία είναι γνωστή ως αρμονική σειρά και η απόκλισή της αποδείχθηκε πρώτη φορά τον 14ο αιώνα (!) από τον Nicolas d'Oresme.
O Euler ξεκίνησε παρατηρώντας ότι

και στη συνέχεια ότι η τιμή της τελευταίας παράστασης όσο περισσότερους όρους προσθέτουμε τόσο πλησιάζει στο 2. Άρα το ζητούμενο άθροισμα βρίσκεται όντως κάπου μεταξύ 0 και 2.
Μετά χρησιμοποίησε το ανάπτυγμα Taylor (ή καλύτερα Maclaurin γιατί το ανάπτυγμα είναι γύρω απ'το σημείο x=0) για τη συνάρτηση ημίτονο:

απ'όπου προκύπτει

Γνωρίζοντας ότι κάθε συνάρτηση που έχει πεπερασμένο πλήθος ριζών μπορεί να εκφραστεί συναρτήσει αυτών, κάνει επέκταση και προσπαθεί να εκφράσει τη συνάρτηση ημίτονο συναρτήσει των άπειρων ριζών της.
Ας υποθέσουμε ότι έχουμε μια συνάρτηση που έχει ακριβώς 3 ρίζες, τις 0, π και -π. Τότε η συνάρτηση περιγράφεται από ένα πολυώνυμο τρίτου βαθμού, το

όπου C μια σταθερά, και με γραφική παράσταση

η οποία φυσικά θα είναι διαφορετική για κάθε τιμή της σταθεράς C.
Αν είχαμε ένα πολυώνυμο με 5 ακριβώς ρίζες, τις 0, π, -π, 2π, -2π τότε το πολυώνυμο θα ήταν το
με γραφική παράσταση

που και πάλι θα είναι διαφορετική για κάθε τιμή της C αλλά θα έχει τις ίδιες 5 ρίζες.
Η συνάρτηση sinx έχει άπειρες ρίζες: 0, π, -π, 2π, -2π, 3π, -3π, ...

Ο Euler εδώ κάνει μια μαθηματική ακροβασία και υποθέτει ότι και η συνάρτηση sinx μπορεί να γραφτεί ως πολυώνυμο συναρτήσει των ριζών της:


και προχωράει στον προσδιορισμό της σταθεράς C βάζοντας στο δεύτερο μέλος όπου x το 0 και στο πρώτο μέλος την τιμή του ορίου



Αντικαθιστά την τιμή της σταθεράς που υπολόγισε


Και προχωράει στην επεξεργασία του τελευταίου άπειρου γινομένου. Δεν τον ενδιαφέρουν (προς το παρόν) όλοι οι όροι του αναπτύγματος οπότε λειτουργεί ως εξής:
Από την πρώτη παρένθεση παίρνει τον όρο που είναι χρωματισμένος και από όλες τις άλλες παρενθέσεις το 1:



και συνεχίζοντας μέχρι το άπειρο καταλήγει ότι:

Όμως ο συντελεστής αυτός πρέπει να είναι ίσος με τον αντίστοιχο συντελεστή στο ανάπτυγμα της σειράς Taylor:

δηλαδή πρέπει


και το πρόβλημα της Βασιλείας λύθηκε!
Για την μαθηματική ακροβασία που ανέφερα παραπάνω ο Euler δέχτηκε επικρίσεις όταν δημοσίευσε το αποτέλεσμά του. Το ωραίο σ'αυτή την ιστορία είναι ότι αργότερα αποδείχθηκε ότι ο Euler χρησιμοποίησε ένα θεώρημα... από το μέλλον! Συγκεκριμένα το θεώρημα παραγοντοποίησης του Weierstrass που αποδείχθηκε περισσότερο από 100 χρόνια αργότερα!
Ο Euler όμως δε σταμάτησε εδώ. Συνέχισε με παρόμοια διαδικασία και βρήκε ότι


και για κάθε άρτιο εκθέτη ότι

Τα παραπάνω αποτελέσματα χρειάζονται στη Φυσική. Για παράδειγμα όταν αποδεικνύουμε στην κβαντική φυσική ότι ο νόμος Stefan-Boltzmann είναι συνέπεια του εμπειρικού τύπου του Planck για τη φασματική κατανομή της ακτινοβολίας μέλανος σώματος.
Ο εμπειρικός τύπος του Planck είναι:

όπου J είναι η φασματική κατανομή της θερμικής ακτινοβολίας για κάποια απόλυτη θερμοκρασία Τ, f η συχνότητα, h η σταθερά του Planck, c η ταχύτητα του φωτός και k η σταθερά του Boltzmann.
Για να υπολογίσουμε την ολική ακτινοβολούμενη ισχύ ανά μονάδα επιφανείας του μέλανος σώματος χρειάζεται ο υπολογισμός του ολοκληρώματος

Ξεκινάμε αναπτύσσοντας τον όρο

χρησιμοποιώντας τον τύπο για τη γεωμετρική σειρά




απ'όπου φαίνεται ότι η ενέργεια της ηλεκτρομαγνητικής ακτινοβολίας πρέπει να είναι ακέραιο πολλαπλάσιο της ποσότητας hf, δηλαδή ότι η ενέργεια είναι κβαντωμένη.
Συνεχίζουμε για τον υπολογισμό του ολοκληρώματος:





Το ολοκλήρωμα υπολογίζεται με διαδοχικές παραγοντικές ολοκληρώσεις:



που είναι ο νόμος Stefan-Boltzmann και βρίσκεται σε απόλυτη συμφωνία με τα πειραματικά δεδομένα. Απόλυτη μαγεία!


Comments
Post a Comment