Ο αριθμός του Όιλερ (Euler's number) - e=2,718...

 

     Φανταστείτε ότι βρισκόμαστε σε μια χώρα όπου οι τραπεζικές καταθέσεις τοκίζονται με επιτόκιο 100%. Αν κάναμε μια κατάθεση 1 ευρώ, μετά από ένα χρόνο θα είχαμε

ευρώ.

Ας υποθέσουμε τώρα ότι η τράπεζα δέχεται να τοκίζει το κεφάλαιο ανά εξάμηνο με 50%. Τότε στο τέλος του πρώτου εξαμήνου θα είχαμε 

 ευρώ και στο τέλος του δεύτερου εξαμήνου 

ευρώ ή ισοδύναμα 

 ευρώ.

Αν ο ανατοκισμός γινόταν ανά τετράμηνο με 33,33% τότε στο τέλος του έτους θα είχαμε 

 ευρώ και ανά τρίμηνο με 25% θα είχαμε 

 

 ευρώ.

Ανατοκίζοντας το κεφάλαιο του ενός ευρώ κάθε στιγμή (θεωρώντας ότι ο χρόνος είναι συνεχής μεταβλητή που διαιρείται επ'άπειρον) προκύπτει το όριο 

που ονομάζεται αριθμός του Όιλερ και συμβολίζεται με e. Το e είναι άρρητος αριθμός (όπως και τα π και φ) και υπερβατικός (όπως και το π αλλά όχι το φ) δηλαδή δεν μπορεί να προκύψει ως ρίζα πολυωνύμου οποιουδήποτε βαθμού με ρητούς συντελεστές.

 

 

    Η ακολουθία

συγκλίνει στο e αλλά σχετικά αργά.

 

    Το e μπορεί να υπολογιστεί από την άπειρη σειρά

 που συγκλίνει πολύ πιο γρήγορα.

    Οι πρώτες αναφορές στον αριθμό e δημοσιεύθηκαν το 1618 σε πίνακα λογαρίθμων από τον Τζον Νάπιερ στον οποίο οφείλουμε το όνομα νεπέριοι λογάριθμοι (ή φυσικοί λογάριθμοι). Ωστόσο ο πίνακας δεν περιλαμβάνει τον ίδιο τον αριθμό αλλά μια λίστα από λογάριθμους που υπολογίζονται από αυτόν. Η ανακάλυψη του αριθμού e πιστώνεται στον Γιακόμπ Μπερνούλι ο οποίος το 1683 προσπάθησε να βρει την τιμή της από την ακόλουθη έκφραση (που είναι στην πραγματικότητα το e): 

 

 

    Ο Leonhard Euler το 1748 υπολόγισε την τιμή του e με 23 ψηφία χρησιμοποιώντας τη σχέση    

 

    Το e εμφανίζεται στον ασυμπτωτικό τύπο του Stirling για το n! για μεγάλες τιμές του n

και μπορεί να προσεγγιστεί μέσω των συνεχόμενων κλασμάτων:

όπου το μοτίβο είναι 2,1,1,4,1,1,6,1,1,8,1,1,10,1,1...

 

το τελευταίο συνεχόμενο κλάσμα συγκλίνει πολύ πιο γρήγορα.

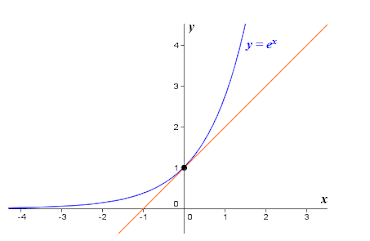
    Η εκθετική συνάρτηση με βάση το e έχει την εξαιρετική ιδιότητα (όπως επίσης και η εκθετική συνάρτηση πολλαπλασιασμένη με οποιαδήποτε σταθερά)

που μπορεί να αποδειχθεί πολύ εύκολα π.χ. από το ανάπτυγμα Taylor

ως εξής:

που σημαίνει ότι η κλίση της γραφικής παράστασης σε οποιοδήποτε σημείο ισούται με την τιμή της συνάρτησης σ´αυτό το σημείο.

πχ για x=0 η συνάρτηση έχει τιμή 1 που είναι ίση με την κλίση της εφαπτόμενης σ´αυτό το σημείο.

    Στη φύση το e εμφανίζεται σε κάθε περίπτωση που ο ρυθμός μεταβολής ενός μεγέθους είναι ανάλογος με την τιμή του μεγέθους την ίδια στιγμή. Μερικές περιπτώσεις που αυτό συμβαίνει:

1. Ραδιενέργεια. 

Ο ρυθμός διάσπασης των ραδιενεργών πυρήνων είναι ανάλογος με το πλήθος των πυρήνων

οπότε προκύπτει

και η σταθερά C υπολογίζεται αν για t=0 έχουμε Νο πυρήνες

 

2. Φόρτιση ή εκφόρτιση πυκνωτή. Με παρόμοια διαδικασία έχουμε

κατά την εκφόρτιση και

κατά τη φόρτιση.

 

3. Σε μερικές χημικές αντιδράσεις ο ρυθμός μεταβολής της συγκέντρωσης ενός αντιδρώντος είναι ανάλογος με τη συγκέντρωση του αντιδρώντος, οπότε προκύπτει εκθετική μείωση.

... και σε πολλές ακόμα περιπτώσεις.

    Επιστροφή στα μαθηματικά για τη σύνδεση του e με τους μιγαδικούς αριθμούς. Από τη σχέση

αντικαθιστώντας το x με ix (i η φανταστική μονάδα) έχουμε

όπου χρησιμοποιήσαμε τα αναπτύγματα Taylor

και

    Από τη σχέση

για x=π έχουμε

και προκύπτει

που θεωρείται "η ομορφότερη εξίσωση" επειδή συνδυάζει 5 θεμελιώδεις αριθμούς:

Το 0, το 1, το π, το i και το e.

    Ο αριθμός του Όιλερ e μερικές φορές συγχέεται με τη σταθερά του Όιλερ ή πιο γνωστή ως σταθερά Euler-Mascheroni που συμβολίζεται με γ και έχει τιμή 

για την οποία δε γνωρίζουμε αν είναι ρητή ή άρρητη. Ο Όιλερ είναι ο μοναδικός μαθηματικός που το όνομά του έχει δοθεί σε δυο σταθερές! Σωστά νομίζω χαρακτηρίστηκε ως "ο Mozart των μαθηματικών".